PHYSICS: Moment of Inertia

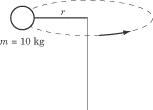
Moment of inertia is a measure of an object’s resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation.

For a point mass the moment of inertia is the mass times the square of perpendicular distance to the reference axis and can be expressed as:

l = mr²            (1)

where l = moment of inertia, m = mass, r  distance between axis and rotation mass.

The point mass relationships are basis for all other moments of inertia since any object can be built up from a collection of point masses.

For rigid bodies with continuous distribution of adjacent particles, the formula is better expressed as an integral.

l = ∫r²dm       (2b)

where dm = mass of an infinitesimally small part of the body

General Formula

l = kmr²          (5)

where k = inertial constant – depending on the shape of the body

SOME TYPICAL BODIES AND THEIR MOMENTS OF INERTIA

Inertia of Cylinder

Thin-walled hollow: comparable with the point mass (1) and can be expressed as:

l = mr²            (3a)

where m = mass of the hollow, r = distance between axis and the thin-walled hollow, r_o = distance between axis and outside hollow.

Hollow:          l = 1/2m (r_i² + r_o²)             (3b)

where m = mass of hollow, r_i = distance between axis and inside hollow, r_o = distance between axis and outside hollow

Solid:              l = 1/2mr²    (3c)

where m = mass of cylinder, r = distance between and outside cylinder

Inertia of Sphere

Thin-walled hollow:                         l = 2/3mr²     (4a)

where m = mass, r = distance between axis and hollow

Solid:              l = 2/5mr²     (4b)

where m = mass, r = radius

Rectangular Plane

Axis through center:

where a, b = short and long sides

Axis along edge:

Slender Rod

Axis through center:

where L = length of rod

Axis through end:

Source: www.engineeringtoolbox.com/moment-inertia-torque-d_913.html

PHYSICS: Rotational Kinematics

ANGULAR POSITION

By convention, we measure angles in a circle in a counterclockwise direction from the positive x-axis. The angular position of a particle is the angle, Φ, made between the lines connecting that particle to the origin, O, and the positive x-axis, measured counterclockwise.

In this figure, point P has an angular position of Φ. Note that every point on the line OP has the same angular position: the angular position of a point does not depend on how far that point is from the origin, O.

We can relate the angular position of P to the length of the arc of the circle between P and the x-axis by means of an easy equation: Φ = L/r; where L = length of the arc, and r = radius of the circle.

ANGULAR DISPLACEMENT

Imagine that the wheel is rotated so that every point on the line OP moves from an initial angular position of Φ_i to a final angular position of Φ_f. The angular displacement, θ, of line OP is: θ = Φ_f – Φ_i

For example, if you rotate a wheel counterclockwise such that the angular position of line OP changes from Φ_i = 45^o = π/4 to Φ_f = 135^o = 3π/4, as illustrated below, then the angular displacement of line OP is 90^o or π/2radians.

For line OP, to move in the way described above, every point along the line must rotate 90^o counterclockwise. By definition, the particles that make up a rigid body must stay in the same relative position to one another. As a result, the angular displacement is the same froe every point in a rotating rigid body.

Note: The angular distance a point has rotated may or may not equal that point’s angular displacement.

ANGULAR VELOCITY, is defined as the change in the angular displacement over time. Average angular velocity, is defined by:

Angular velocity is typically given in units of rad/s. As with angular displacement, the angular velocity of every point on a rotating object is identical.

ANGULAR ACCELERATION, a, is defined as the rate of change of angular velocity over time. Average angular acceleration, ā, is defined by:

Angular acceleration is typically given in units of rad/s².

Sources: www.sparknotes.com/

PHYSICS: Rotational Motion

Rotational motion deals with the rotation of a body or an object about its center of a mass. The movement of any object can be described through the combination of translational motion of the object’s center of mass and its rotational motion about that center of mass.

ANGULAR MOMENTUM

We can define angular momentum in terms of moment of inertia and angular velocity, just as we can linear momentum in terms of mass and velocity: L = Iw.

The angular momentum vector always points in the same direction as the angular velocity vector.

Angular Momentum of a Single Particle

Example: Tetherball of mass m swinging about on a rope of length r:

The tetherball has a moment of inertia of I = mr² and an angular velocity of �� = v/r.

Substituting these values into the formula for linear momentum we get:

The momentum, p = mv of a particle moving in a circle is always tangent to the circle and perpendicular to the radius. Therefore, when a particle is moving in a circle,

Sources: www.sparknotes.com/

PHYSICS: Conservative and Non-conservative Forces

When a conservative force does work, you can get that energy changes forms, whether a conservative force does work or non-conservative does work. But when a conservative force does work, it’s easy to get the energy out of the system. And when a non-conservative force does work, it’s much tougher to get the energy out of the system.

To determine whether an object has conservative force or non-conservative forces:

1.       The work done by a conservative force when displacing an object from point “a” to point “b” is independent of the path taken.

·         Friction is a non-conservative force.

2.     The work done by a conservative force over a closed path is always zero.

Example, in the problem of free fall (neglecting air drag) we have already studied, an object is thrown upward at a certain initial speed. It reaches a maximum height where its velocity is zero and then starts to descend with negative velocity. Clearly the body has lost all its kinetic energy once it has reached the maximum height, because it has zero velocity. However, as the objects falls back, when it reaches the ground again its speed is identical to its initial speed. What happened is that on the way up the force of gravity does a negative work on the object, while on the way down it does a positive work, giving back to the object the same energy it had taken away. Forces like this are called conservative, because their work is never wasted, it can always be recovered. Forces that are not conservative, whose work cannot be recovered, are called non-conservative. The best examples are friction and air drag. Non-conservative forces tend to disperse their work into forms that cannot be recovered by simply reversing the motion, such as heat and sound.

It is useful to recast the work-energy theorem in a new way based on the distinction of conservative and non-conservative forces. The theorem was: W = ΔKE

Now we can rewrite this as:

WNC + WC = ΔKE

because the net work is the sum of the work of conservative and non-conservative forces.

Understanding Conservative Forces

·         The object regains initial motion (kinetic energy) on return to initial position in a closed path motion.

·         Conservative force transfers energy "to" and "from" an object during a closed path motion in equal measure.

·         Conservative force transfers energy between kinetic energy of the object in motion and the potential energy of the system interacting with the object.

·         Work done by conservative force is equal to work done by it on reversal of motion.

·         Total work done by conservative force in a closed path motion is zero.

Understanding Non-conservative Forces

·         The speed and kinetic energy of the object on return to initial position are lesser than initial values in a closed path motion.

·         Non - conservative force does not transfers energy "from" the system "to" the object in motion.

·         Non - conservative force transfers energy between kinetic energy of the object in motion and the system via energy forms other than potential energy.

·         Total work done by non-conservative force in a closed path motion is not zero.

Sources: www.youtube.com/

http://cass246.ucsd.edu/

http://cnx.org/content/m14104/latest/

PHYSICS: Kinetic Energy

Kinetic energy is the energy in motion. An object that has motion – whether it is vertical or horizontal motion – has kinetic energy. These are many forms of kinetic energy – vibrational (the energy due to vibrational motion), rotational (due to rotational energy), and translational (due to motion from one location to another). Focusing on translational, the following equation is used to represent the kinetic energy (KE) of an object:

Where, m = mass of object

v = speed of the object

This equation reveals that the kinetic energy of an object is already proportional to the square of its speed. That means, for a twofold increase in speed, the kinetic energy will increase by a factor of four. For a threefold increase in speed, the kinetic energy will increase by a factor of nine. And for a fourfold increase speed, the kinetic energy will increase by a factor of sixteen. The kinetic energy is dependent upon the square of the speed.

Kinetic energy is a scalar quantity; it does not have a direction. The kinetic energy of an object is completely described by magnitude alone. The standard metric unit of measurement for kinetic energy is the Joule – one Joule is equivalent to 1kg*(m/s) ^2.

Equations:

Linear motion:

Rotational motion:

where, cor means center of rotation, and com is the center of the mass.

Conservation of energy:

Linear motion (relativistic):

where the final approximate equality holds for v << c.

Extended Explanation:

When a (non-relativistic) particle of mass moves with velocity, the particle’s kinetic energy is given by

The relationship between the momentum p and velocity is p = mv equation (1) can also be written

For a collection of particles (labeled by index) the total kinetic energy is given by

where m_(i) is the mass of the ith particle and v_{(i)} is the magnitude of the ith particle’s velocity.

For the case of a continuous distribution of particles

For the case of the rigid body v(r) = ω x r for constant ω, and the above equation reduces to

where

In many cases (e.g., cubic, spherical) the system is symmetric enough that

in which case the above equation for kinetic energy reduces to

Sources: www.physicsclassroom.com/class/energy/

www.physics forums.com/

PHYSICS: Potential Energy

Potential energy exits whenever an object which has mass has a position within a force field. An object can store energy as the result of its position. Potential energy is the stored energy of position possessed by an object.

Gravitational Potential Energy

-         Is the energy stored in an object as the result of its vertical position or height. The gravitational potential energy of the massive ball of a demolition machine is dependent on two variables – the mass of the ball and the height to which it is raised. There is a direct relation between gravitational potential energy and the mass of an object. More massive objects have greater gravitational potential energy. There is also a direct relation between gravitational potential energy and the height of an object. The higher that an object is elevated, the greater the gravitational potential energy. These relationships are expressed by the following equation:

m = mass of the object

h = height of the object

g = gravitational field strength (9.8 N/kg)

Elastic Potential Energy

-         Is the energy stored in elastic materials as the result of their stretching or compressing. The amount of elastic potential energy stored in such a device is related to the amount of stretch of the device – the more stretch, the more stored energy.

Springs are a special instance of a device that can store elastic potential energy due to either compression or stretching. A force is required to compress a spring; the more compression there is, the more force that is required to compress it further. For certain springs, the amount of force is directly proportional to the amount of stretch or compression (x); the constant of proportionality is known as the spring constant (k).

Such spring are said to follow Hooke’s law. If a spring is not stretched or compressed, then there is no elastic potential energy stored in it. The spring is said to be at its equilibrium position. The equilibrium position is the position that the spring naturally assumes when there is no force applied to it. In terms of potential energy, the equilibrium position could be called the zero-potential energy position. There is a special equation for springs that relates the amount of elastic potential energy to the amount of stretch (or compression) and the spring constant. The equation is:

k = spring constant

x = amount of compression

(relative to equilibrium position)

Source: www.physicsclassroom.com/class/energy/

PHYSICS: Gravitation

Gravitation in everyday life is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped. Most people are familiar with gravity as the reason behind things staying on the earth’s surface, or “what goes up, must come down,” but gravity actually has a much vaster significance. Gravity is responsible for the formation of our earth and all other planets and for the movement of all heavenly bodies. It is gravity that makes our planet revolves around the sun and the moon revolve around the earth.

Newton’s first law states that the force of gravity between two masses is directly proportional to the product of the two masses and inversely proportional to the square of the distance between them, or mathematically: F = G(m₁m₂/d²), where G is a constant. Newton’s second law states that gravitational force is equal to the product of a body’s mass and its acceleration, or F = ma.

Formulas:

Universal Law of Gravitation

Where m₁ and m₂ are the masses of any two objects under consideration and r₁ and r₂ are their respective position vectors.

Equation for the gravitational constant

Sir Isaac Newton:

Weight and the Gravitational Force

Sources: www.wisegeek.com/

www.sparknotes.com/physics/gravitational/

www.csep10.phys.utk.edu/

PHYSICS: Free Fall

A free falling object is an object that is falling under the sole influence of gravity. Any object that is being acted upon only by the force of gravity is said to be in a state of free fall. There are two important motion characteristics that are true of free-falling objects:

• Free-falling objects do not encounter air resistance.
• It accelerates downwards at a rate of 9.8 m/s².

Because free-falling objects are accelerating downwards at a rate of 9.8 m/s², a dot diagram of its motion would depict acceleration. The dot diagram at the right depicts the acceleration of a free-falling object. The position of the object at regular time intervals – say, 0.1 second is shown. The fact that the distance that the object travels every interval of time is increasing is a sure sign that the ball is speeding up as it falls downward. An object travels downward and speeds up, and then its acceleration is downward.

Uniform Gravitational Field without Air Resistance

Where:
     v₀ – is the initial velocity (m/s)

     v(t) – vertical velocity with respect to time (m/s)

     y₀ – initial altitude (m)

     y(t) – altitude with respect to time (m)

     t – time elapsed

     g – acceleration due to gravity

Problem ~

An object in free fall is said to have reached terminal velocity. If the air resistance becomes strong enough to counter act all gravitational acceleration, causing the object to fall at a constant speed. The exact value of the terminal velocity varies according to the shape of the object, but can be estimated for many objects at 100m/s. When a 10kg object has reached terminal velocity, how much power does the air resistance exert on the object?

Solution:
To solve this problem, we will use the equation P = Fv cos θ instead of the usual power equation, as we are given the velocity of the object. We merely need to calculate the force exerted on the object by the air resistance, and the angle between the force and the velocity of the object. Since the object has reached a constant speed, the net force on it must be zero. Since there are only two forces acting on the object, gravity and air resistance, the air resistance must be equal in magnitude and opposite in direction as the force of gravity. Thus, F_a = - F₆ = mg 98N , pointing upwards. Thus, the force applied by air resistance is anti-parallel to the velocity of the object. Thus:

Sources: www.physicsclassroom.com/

www.sparknotes.com/physics/workenergypower/